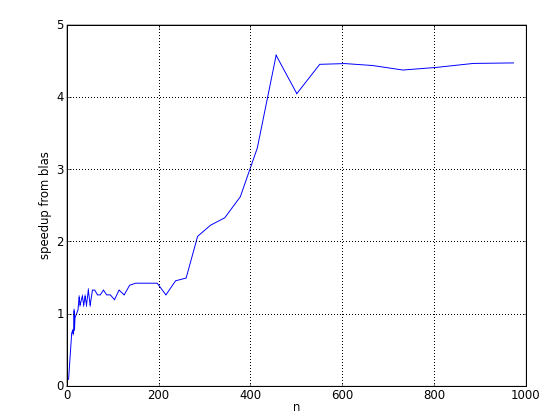
Matrix multiplication speeds in C

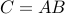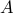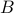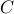The following graphs compare naïve and (non-ATLAS) BLAS implementations of matrix multiplication in C. They use the same Intel Core Duo Linux machine at 1.66GHz. The computation is , where , and are all full matrices in 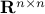. For the smaller matrices, at least one second was spent repeating the multiplication, to get a higher precision result.

Code was compiled with gcc 4.3.1 and options -O2 -funroll-loops. No performance improvement was observed with -O3. (See computation speeds for some reference measurements on the same computer.)

for (i = 0; i < n; i++)
    for (j = 0; j < n; j++) {
        C[i + j*n] = 0;
        for (k = 0; k < n; k++)
            C[i + j*n] += A[i + k*n]*B[k + n*j];
    }

dgemm_(&charN, &charN, &n, &n, &n, &one_d, A, &n, B, &n, &zero_d, C, &n);

For comparison, a simple multiply-add was timed with vectors of length 200 (ie, using level 2 cache only). This reference time was scaled by 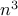and plotted on the same chart below. Apparently BLAS even schedules instructions better than would be possible by just repeating this primitive operation.

z[i] += x[i] * y[i];

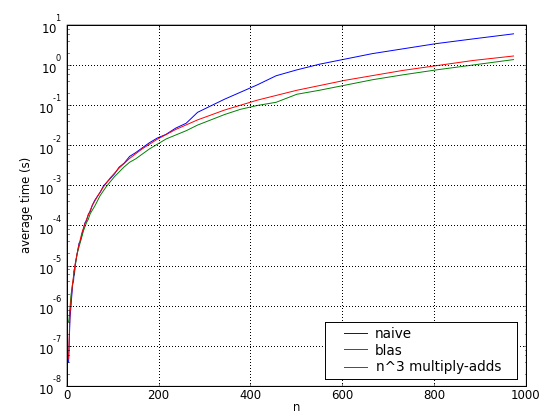
Multiplication time

(All three graphs are the same: the first and second use (different) logarithmic scales on the y-axis, while the second has logarithmic scales on both the x- and the y-axes.)

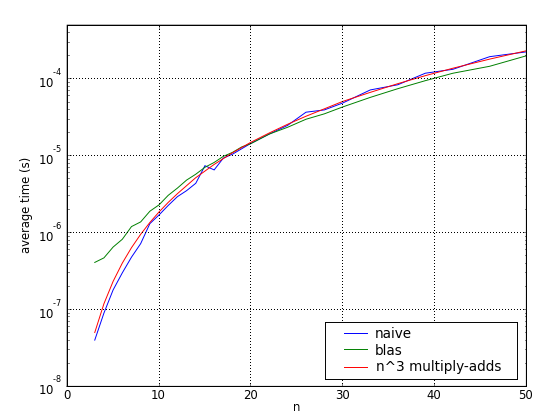
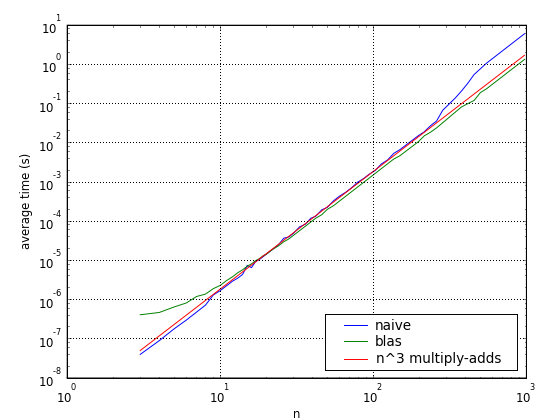
Speedup