Extremely short Matlab LP solvers

49 characters: ADMM-based solver

This one by Borja Peleato is based on ADMM, does not require any particular initialization, and uses just 49 characters. (Yes, that is indeed ridiculously short.)

for i=1:99,z=max(z-x,x-c);x=z+pinv(A)*(b-A*z);end

69 characters: More stable than the original version

Zhonghao Zhang, a student of Chee Wei Tan, emailed me in November 2010 with this solver:

for i=1:50,X=diag(x);F=X*null(A*X);d=F*F'*c;x=x-d/max(X\abs(d))/2;end

It is a mere 69 characters (though uses the higher-level function ‘null’), and seems more stable than my solver.

75 characters: The original version

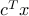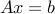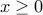This is Dikin's method for minimizing , subject to and . Start with x at a feasible point.

for i=1:50,p=diag(x)^2;r=p*(c-A'*(A*p*A'\A*p*c));x=x-r*min(x./abs(r))/2;end

A = randn(100, 300);
x0 = rand(300, 1);
b = A*x0;
c = rand(300, 1);
x = x0;
for i=1:50,p=diag(x)^2;r=p*(c-A'*(A*p*A'\A*p*c));x=x-r*min(x./abs(r))/2;end

Astonishingly, this particular solver continues to get smaller and smaller, with the latest reduction placed here in March 2010 (down from 80 characters). Thanks to Yang Wang and Richard Brown for suggesting improvements. Let me know if you can reduce it further!